Grandeurs Alternatives et Sinusoïdales
Introduction
Bon, on a vu plein de choses sympas sur le courant, la tension et les résistances. Le problème, c'est que ce n'est que le début, et vous allez devoir vous accrocher.
Pour plein de raisons pratiques, c'est beaucoup plus simple (et surtout moins cher) d'utiliser des signaux sinusoïdaux. Donc 1er conseil, si vous n'avez pas encore fait de barbecue avec, retournez chercher dans vos cours de terminale tout ce qui touche à la trigonométrie et révisez le!!
En ce qui concerne les signaux, nous allons commencer avec le début (logique non?) :
2ème conseil : Retenez bien les unités, parce que les profs vous enlèveront la moitié des points à chaque fois que vous ne les indiquez pas, et ils auront parfaitement raison. Mais revenons à nos moutons…
3ème conseil : retenez bien ce qui arrive, car c'est fondamental.
Quelques notions
Tout signal sinusoïdal possède une période T. Cette période T se mesure en seconde. Pour ceux qui ne s'en souviennent plus, la période représente le temps que le signal met à se répéter.

Normalement, ce schéma doit réveiller en vous deux ou trois souvenirs de physique.
Mais en général, on ne se sert pas trop de la période, on préfère utiliser la fréquence. La fréquence ; c'est l'inverse de la période et elle se note f; donc f = 1/T et f s'exprime en Hz.
J'espère que pour vous, tout ça relève de la révision, car maintenant on se lance dans le nouveau.
La pulsation. Elle se note ω. Et ω=2.π.f et son unité est le radian/seconde que l'on notera rad/s pour aller plus vite.
Je sais que vous êtes en GEII et que vous en avez marre que je ne vous parle pas de courant ou de tension. Mais ça arrive, ne vous inquiétez pas.
Ce que je vais vous raconter maintenant concerne la tension, mais vous pouvez aussi l'appliquer au courant (et de toute façon, vous serez obligé de le faire).
Dans un signal, on va s'intéresser à plusieurs valeurs particulières de celui-ci.
Tout d'abord, la valeur crête. Ne cherchez pas compliqué, c'est la valeur maximale qu'atteint votre signal. Elle se note avec un ‘‘chapeau’’ au-dessus du V :
Puis la valeur moyenne. Normalement ce mot vous dit quelque chose. On la note Vmoy ou V. Que puis-je vous dire dessus? Pas grand-chose à part qu’elle représente le "milieu" du signal.
Et enfin la Valeur crête à crête du signal. On l'appelle parfois amplitude et se note Vcac (faut dire qu'on ne cherche pas trop dans l'originalité), elle représente la distance (sur l'axe vertical) entre Vmax et Vmin . Attention : ce n'est pas 2 x Vmax !! Pour ceux qui sont un peu plus matheux, retenez que pour un signal donné, Vcac = Vmax - Vmin.
Ah oui, Vmin c'est la valeur la plus faible du signal.

Ci-contre, vous pouvez voir plus ou moins à quoi elles ressemblent .
Représentation d'un signal
Mais comment représenter un signal sinusoïdal? Haha ! Rien de plus simple. Alors déjà, on sait que notre signal a une forme sinusoïdale et on va lui attribuer une fréquence fixe dans le temps. Et qui dit fréquence, dit pulsation. Je ne vous explique pas pourquoi, c’est un peu long et fastidieux, mais on utilisera toujours la pulsation.
Il sera donc de la forme sin(ωt). Cependant, un sinus, ça varie entre 1 et -1 (pour ceux qui n'en sont pas convaincus, (retourner voir vos cours de terminale ou de première). Et autant vous dire que vous n'irez pas bien loin avec cela.
Du coup on multiplie notre signal par la valeur max qu'on veut lui donner (donc Vmax).
Notre signal est donc de la forme Vmax*sin (ωt). Facile? Tant mieux.
La Valeur Efficace
C'est la chose la plus importante!!!! Mais quelle est cette chose si importante?
Eh bien chez vous, tout ce que vous branchez sur le secteur est alimenté par une source de tension sinusoïdale .
La Valeur efficace est la tension qu’il me faut si je veux alimenter mon montage en continu.
Prenons l'exemple de votre lampe de bureau (ou celle du plafond, c'est pareil), elle émet toujours la même lumière.
Maintenant, vous décidez d'alimenter votre lampe avec cette source d'alimentation continue (je sais que c'est débile, mais c'est essentiel pour comprendre la suite).
Mais comment connaitre la valeur efficace? Je vous donne sa formule : Veff = Vmax/√2
Prenons un exemple (j'aime bien les exemples) :

Vous achetez un lave-linge pour votre appartement. Vous pourriez très bien le brancher au réseau 325 V et vous dire que c'est fini. (je ne me suis pas trompé, j'ai bien dit 325 V)
Mais vu que vous êtes en GEII vous vous demandez : "Et si j'utilisais une alimentation pour calculer la valeur de la tension qui me permettrait d'alimenter mon montage avec une tension continue ?" (si vous vous demandez vraiment ça, pensez à consulter un psy dès que possible).
Donc à ce moment-là, vous prenez votre calculatrice et vous tapez : 325/√2 = 230 Volts. Voilà, vous savez que vous pouvez alimenter votre circuit avec une source de tension continue de 230 Volts.
En fait, vous avez toujours entendu parler de la valeur efficace, mais vous ne saviez pas ce que c'était... #Révélation
Dit comme ça Veff semble inutile puisque l'on ne sert presque jamais de tensions continues. Mais elle va vous simplifier les calculs dans bien des cas…
Je vous raconte un dernier petit truc et je vous explique à quoi elle sert.
Vous vous souvenez de la loi d'Ohm (j'espère très sincèrement pour vous que oui). Maintenant qu'on va alimenter nos circuits avec des tensions sinusoïdales, on devrait se retrouver avec des expressions du genre sin(ωt) de partout. Eh bien non! Car au lieu d'écrire sinus (machin) et sinus (truc) de partout, on peut utiliser les valeurs efficaces.
Prenons encore un exemple :

J'ai une source de tension qui délivre une tension sinusoïdale telle que : E(t)=Emax*sin(ωt)
J'ai donc un courant sinusoïdal de la forme : I(t)=Imax*sin(ωt). Mes résistances ont une valeur en Ω qui, elle, est constante.
Imaginons que je m'intéresse à U1 :
D'après la loi des mailles, j'ai U1(t) = Emax*sin(ωt)
Et d'après la loi d'Ohm: U1(t) = Imax*sin(ωt) x R1.
On est d'accord pour dire que c'est un peu pénible à utiliser?
Tandis que si j'utilise les valeurs efficaces ; je peux écrire :
U1eff = R1 x Ieff. C'est déjà plus joli non?
Petit exercice d'application :
Toujours sur le même circuit : On cherche à déterminer R1. On donne : E(t)=15.sin(ωt) et I(t)=2.sin(ωt)
1. Identifier Umax et/ou Imax
On voit donc que U1max = 15 V et Imax = 2 A.
2. Calculer Ueff et/ou Ieff
On calcule U1eff = 15/√2 =10,6 V et Ieff = 2/√2 = 1,41 A
3. On applique les théorèmes dont on a besoin
On applique la loi d'Ohm et pouf! Ueff=R1.Ieff => R1 = Ueff / Ieff = 10,6/1,41 = 7,5 Ohms
Voilà, on a trouvé la valeur de notre résistance.
Attention!! A tous les petits malins qui ont remarqué que les sin(ωt) pouvaient se simplifier et qu'en utilisant les valeurs max des signaux on trouvait la même résistance. Ça ne marche pas!!! En effet, il reste deux notions que je ne vous ai pas encore présenté pour les signaux et qui fausseront vos calculs dès qu'elles apparaîtront. Donc respecter scrupuleusement la méthode décrite ci-dessus.
Pour l'instant, nous avons étudié des signaux classiques. Vous aurez affaire à eux la plupart du temps. Mais bon, il existe quand même d'autres cas assez répandu pour que nous soyons obligés de les traiter.
Je commence avec la plus facile. La composante continue : comme son nom l'indique, il s'agit d'une composante continue, mais cette dernière vient s'ajouter au signal.
Voici un exemple :
Imaginons qu'on ait une source de tension qui délivre un signal triangulaire (ça marche avec toutes les formes de signaux) et une autre qui délivre une tension continue.
La composante continue
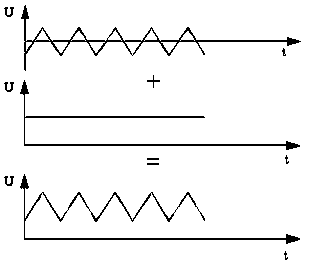
Eh bien la somme des deux nous donne … La somme des deux. Je ne vois pas trop comment vous l'expliquer autrement qu'avec le graphique ci-contre.
En fait, faire la somme des deux revient à "élever" le signal de la valeur de la tension continue .
Pour représenter un signal, on écrira alors : Vmax.sin(ωt) + V' (ce sera toujours sinus ).
Petite astuce pour les flemmards, pour tout signal périodique, la composante continue représente sa valeur moyenne.
Regardons ce sinus
Vous êtes d'accord avec moi pour dire que sa valeur moyenne vaut 0?
Eh bien c'est par ce que ce signal s'écrit : 2.sin(ωt) + V' et que V' = 0.

Aller! Accrochez-vous encore un peu, on a fait le plus dur.
Le déphasage

Nous avons vu, jusqu'à maintenant, que les signaux pouvaient se représenter de la manière suivante : Vmax.sin(ωt) + V'
En fait, ce n'est pas très exact. Un sinus par définition, passe par l'origine du graphique (sin(0)=0 –je vous laisse vérifier à la calculatrice -)
Cependant, (on verra juste après pourquoi), nos signaux ne démarreront pas toujours au temps t0 = 0.
Ils seront un peu décalés. Regardons le schéma qu'il y a au-dessus : on voit bien que les signaux ne sont pas en phases (alors qu'ils ont la même fréquence) : le rouge "démarre" après le bleu.
Et ça, vous allez le rencontrer souvent (je vous explique pourquoi dans quelques lignes).
En gros, le déphasage, c'est la mesure du décalage entre les courbes.
Il se mesure en degré ou en radian et se note α. Il est toujours compris entre -180° et 180°.

On ne sait calculer que la valeur absolue du déphasage. Pour le signe, on fera appelle au bon sens.
Voici la formule qui donne le déphasage :
Normalement vous savez mesurer T. Mais t1? On cherche deux points identiques (en général, on prend le point qui coupe l'axe des abscisses), et on mesure l'écart de temps qu'il y a entre ces deux-là.

Le signe du déphasage : Eh bien, on regarde si la courbe qui nous intéresse est en avance ou en retard sur l'autre.
Par exemple, si je m'intéresse au déphasage de la courbe rouge par rapport à la courbe bleue : on voit bien que la courbe rouge est en retard, donc on met un signe "-" devant notre déphasage.
Mais, si je m'intéresse au déphasage de la courbe bleue par rapport à la courbe rouge, on voit bien que la courbe bleue est en avance, on met donc un signe "+" devant.
Pour le représenter dans l'expression mathématiques de nos signaux; on notera le déphasage α.
Donc au final, pour un signal donné, est expression est : Vmax.sin( ωt + α) + V'
La représentation de Fresnel
On va faire un peu de géométrie. On va représenter nos signaux avec des vecteurs. Pour cela, on va avoir besoin de connaitre la valeur efficace et le déphasage.
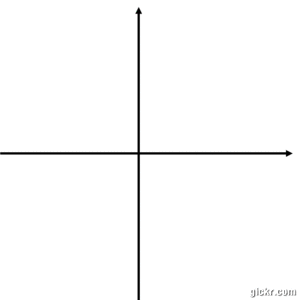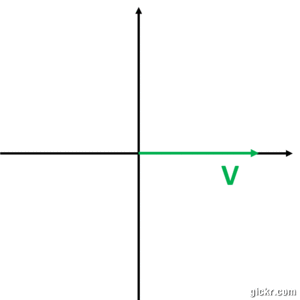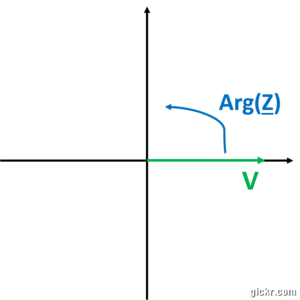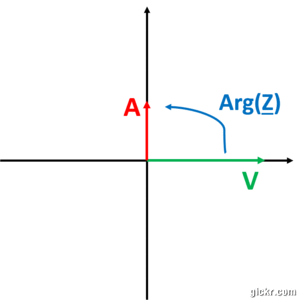
Le but c'est d'avoir quelque chose qui ressemble à ça :
Et vous allez voir, ce n'est pas compliqué du tout.
Mais comment tracer ce magnifique trait rouge?
Alors d'abord, retenez que la longueur du trait rouge vaut sa valeur efficace.
Puis, pour déterminer l'angle, au prend le déphasage.

Du coup, ça donne ça :


Par convention, dans un diagramme de Fresnel, on considère la tension comme origine des phases, il faudra donc la représenter sur l'axe des abscisses. Puis ensuite tracer le courant.
Pour le déphasage, faites bien attention!!! On utilise toujours le déphasage courant/ tension; ce qui revient à utiliser le déphasage de l’impédance (on va voir tout de suite ce que c’est) et on tourne dans le sens trigonométrique!
Vers une nouvelle écriture
Normalement, tout ce que l'on a vu jusqu’à maintenant devait vous parler plus ou moins.
Mais là, je vais me lancer dans un truc un peu plus abstrait. Nous allons découvrir la notion d'impédance complexe. Pour faire simple, essayez de vous dire que c'est une résistance, mais on va ajouter des complexes (vous vous souvenez de i²=-1?). Elle se note Z. Pensez bien à souligner votre terme, sinon ça ne veut rien dire.
Vous vous souvenez de la loi d'Ohm? U = R.I
Eh bien avec l'impédance on a toujours la même chose; sauf que pour marquer l'écriture "complexe", on souligne tous les termes. U= Z.I
Toutes les valeurs que nous allons voir maintenant sont caractérisés par deux propriétés : leur module et leur argument.
Le module se note |Z| = |V| / |I| = Veff/Ieff En fait, le module représente la valeur efficace de l'impédance.
Puis vient l'argument, qui lui, représente le déphasage du courant par rapport à la tension.
On le note arg(Z) (arg qui signifie argument –cours de maths en terminale-)
C'est bien beau tout ça, mais ça ne vous aide pas trop.
Z = [module (en Ω) ; argument (en °)] On appelle cette écriture: "écriture polaire".

On va prendre un exemple :
En alimentant une charge, on a relevé la tension et le courant la traversant.
Cependant, on aimerait bien déterminer la valeur de cette charge; c'est à dire son impédance.
Je vous laisse trouver que le module : |Z|= 2Ω
Pour l'instant j'espère que ça va. Puis c'est parti pour l'argument.
On peut lire sur la courbe que la période du signal est de T= 20 ms = 0.020 seconde.
On peut aussi lire que le courant est en avance de 5 ms = t1 par rapport à la tension.
On obtient alors

Sauf que le courant est en avance, donc on met un signe "+".
Mais comment déterminer l'argument de Z ?
Nous allons découvrir comment faire des calculs avec des coordonnées polaires.
Donc un polaire; ca se note comme ça : [module (en Ω) ; argument (en °)]
On utilisera cette notation uniquement pour les multiplications et les divisions.
Pour les additions et les soustractions, on utilisera la notation rectangulaire (z = a +bi -d'ailleurs, on ne va plus l'appeler "i" mais "j", sinon on risque de le confondre avec le courant et c'est pas génial génial-).
Ne nous égarons pas trop, revenons aux calculs en polaire.
En fait c'est très simple, il faut juste se faire à l'idée :
Lorsque l'on multiplie deux nombres polaires : on multiplie les modules entre eux et on additionne les dépahasages.
Lorsque l'on divise deux nombres polaires : on divise les modules entre eux et on soustrait les déphasages.
Prenons un exemple :
[30;45°]*[10; -25°] = [30*10 ; 45 - 25] = [300 ; 20°]
[25; 35°]/[5; 10°] = [25/5 ; 35-10] = [5;25°]
Eh voilà!!
Donc revenons à ,notre exercice.
On considère la tension comme origine des phases, je peux donc écrire : V=[2/√2 ; 0°] (Origine des phases = Pas de déphasage).
On a vu que le courant était déphasé de 90° par rapport à la phase, on peut donc écrire : I = [1/√2; +90°]
Donc si j'applique ma loi d'Ohm (version Impédance) : V = Z.I donc Z = V / I
On peut alors en déduire :
Z = [2/√2 V ; 0°] / [1/√2 A ; 90°] = [2/1 ; 0 - 90] = [ 2 Ω ; -90°]
Voili voilou; c'était pas si horrible.
Maintenant, je veux tracer le diagramme de Fresnel.
Donc on commence par tracer la tension (moi, je ne mets pas d'échelle, c'est pas pratique à faire sur un site Internet, mais vous, vous serez obligés! Mouhahahahahahahaha).
Maintenant, pour placer le courant, vous partez de votre tension et vous tournez sur votre cercle trigo d'autant de degré que le module de l'impédance.
Vous tracez ensuite le courant (sans oublier l'échelle)!!!
Des nouveaux composants
Je vous ai bassiné un moment avec les impédances, mais vous vous demandez certainement pourquoi? Eh bien on va découvrir des nouveaux composants, qui eux, implique toujours l'apparition d'un déphasage entre le courant et la tension.Oui je sais c'est un peu ch****, mais bon. Donc ces composants...
Eh bien ce sont les condensateurs et les inductances.
On va commencer avec les inductances. En gros, c'est un ralentisseur de courant : a chaque fois qu'on en place une, le courant est retardé par rapport à la tension.
Voici son symbole :

On la note L et elle se mesure en Henry.
C'est le gros cylindre que vous avez en TP. On l'appelle aussi bobine ou self.
Et les condensateurs, c'est l'inverse de l'inductance : c'est un ralentisseur de tension.
Voici son symbole :
On le note C et il se mesure en Farads.
Eh bien pour ces composants, ils n'ont pas de résistances, mais une impédance!! Et maintenant on va se servir de tout ce que l'on a vu dessus.
L'impédance s'exprime toujours en Ohms, pas en Henry, ni en Farads! Ok?
L'impédance d'un condensateur vaut : Z = -j/Cω (je vous rappelle que le j c'est la même chose que i, et c'est pas le courant).
L'impédance d'une inductance vaut Z = jLω.
Réactances et Admittances
On a déja vu qu'une impédance peut se noter Z = a +bj.
On appelle réactance la formule la vaaleur de la partie imaginaire de l'impédance et elle se note X
Pour les matheux, on peut écrire : X = Im(Z)
Vous le verrez par la suite, elle sert dans plein de calculs. Son unité reste le Ohm, et juste le Ohm, et rien d'autre.
Il existe aussi l'admittance. Elle est un peu moins utilisée, mais je vous la donne quand même.
Elle se note Y = 1/Z
Son unité est le Siemens.

Voici un tableau qui vous résume ce qu'il faut savoir sur les impédances.
Il est à connaitre par coeur!!!!
Il ne vous reste plus qu'a vous entrainez!!
